그래프 Graph
그래프란? 정점(Vertex)의 집합과 이들을 연결하는 간선(Edge)의 집합으로 구성되어있다.
주로 선형 자료구조나 트리로 표현하기 어려운 M:N 관계를 표현하기 위해 주로 사용됩니다.
트리도 그래프의 한 종류이다.

✅ 용어
정점(Vertex) :노드(node), 데이터 저장
간선 (Edge) : 정점을 연결하는 선
분지수(차수, degree) : 무방향 그래프에서 하나의 정점에 붙어있는 간선 개수
내향 분지수 (진출 차수, in-degree): 방향 그래프에서 들어오는 간선의 수
외향 분지수(진입 차수, out-degree): 방향 그래프에서 나가는 간선의 수
인접
- 인접(adjacent) : 정점 사이 간선이 있음
- 부속(incident) : 정점과 간선 사이 관계
경로(path) : 출발지에서 목적지로 가는 순서
단순 경로(simple path) : 경로 중 반복되는 정점이 없음. 한붓그리기처럼 같은 간선을 지나지 않음
사이클(cycle) : 단순 경로의 출발지와 목적지가 같은 경우
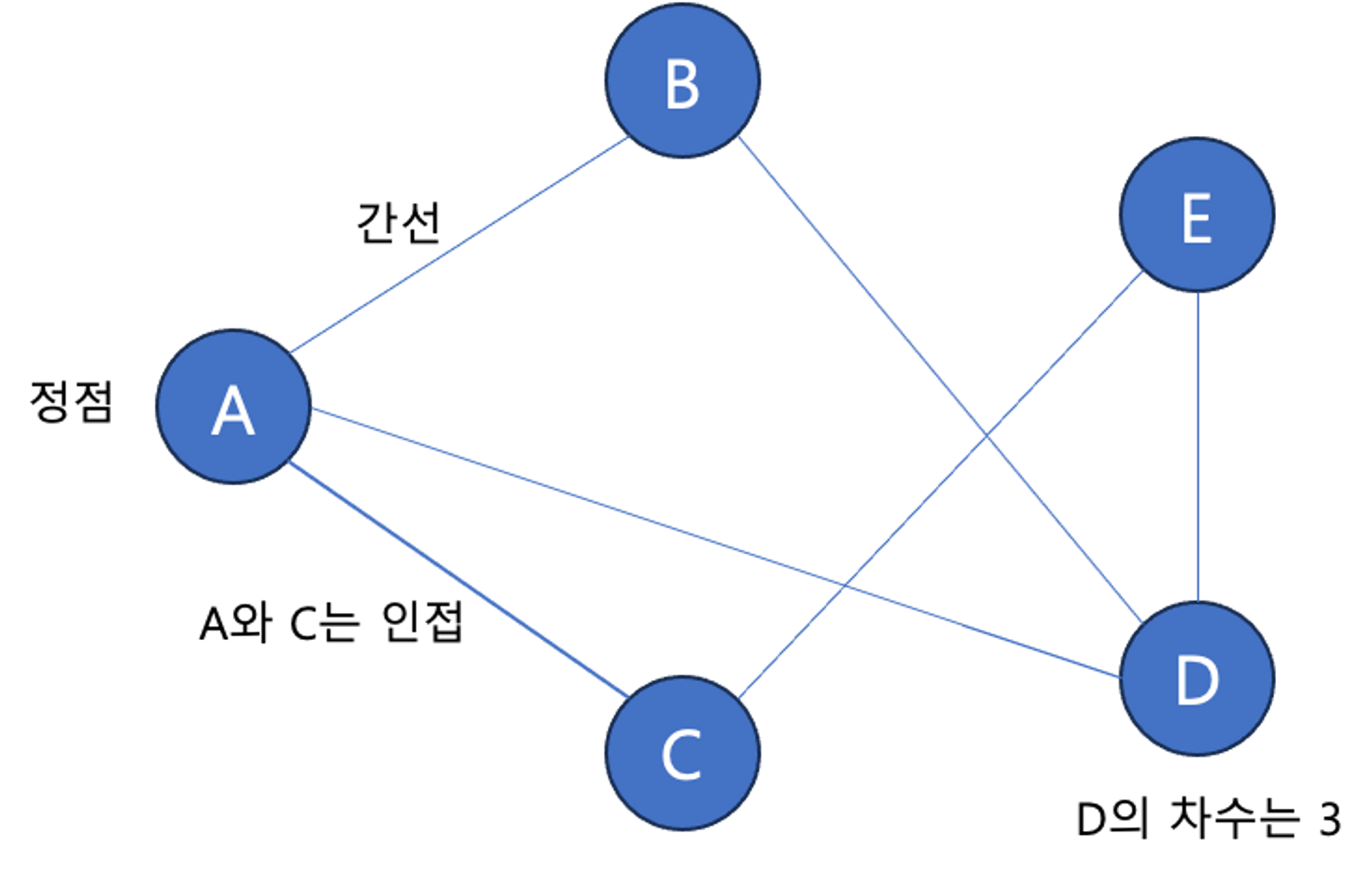
✅그래프 종류
그래프는 연결된 방식에 따라서 다양하게 구분할 수 있다.
- 무향 그래프(Undirected Graph) vs 유향 그래프 (Directed Graph)

- 유향 그래프 : 간선이 방향을 가져서, 한쪽 정점에선 다른 정점에 도달 할 수 있지만, 반대 방향으로는 도달할 수 없는 간선으로 구성된 그래프
- 무향 그래프 : 양쪽 정점에서 간선을 통해 도달하는 것이 자유로운 경우
- 가중치 그래프 (Weighted Graph)

간선에 값을 추가한 그래프, 최단 거리를 구하는 문제 등에서 간선을 택할 때 비용을 추가하는 방식으로 활용할 수 있다.
A에서 E까지의 최단 비용
지도에서 각 지역 간의 거리
- 순환 그래프 (Cycle Graph)
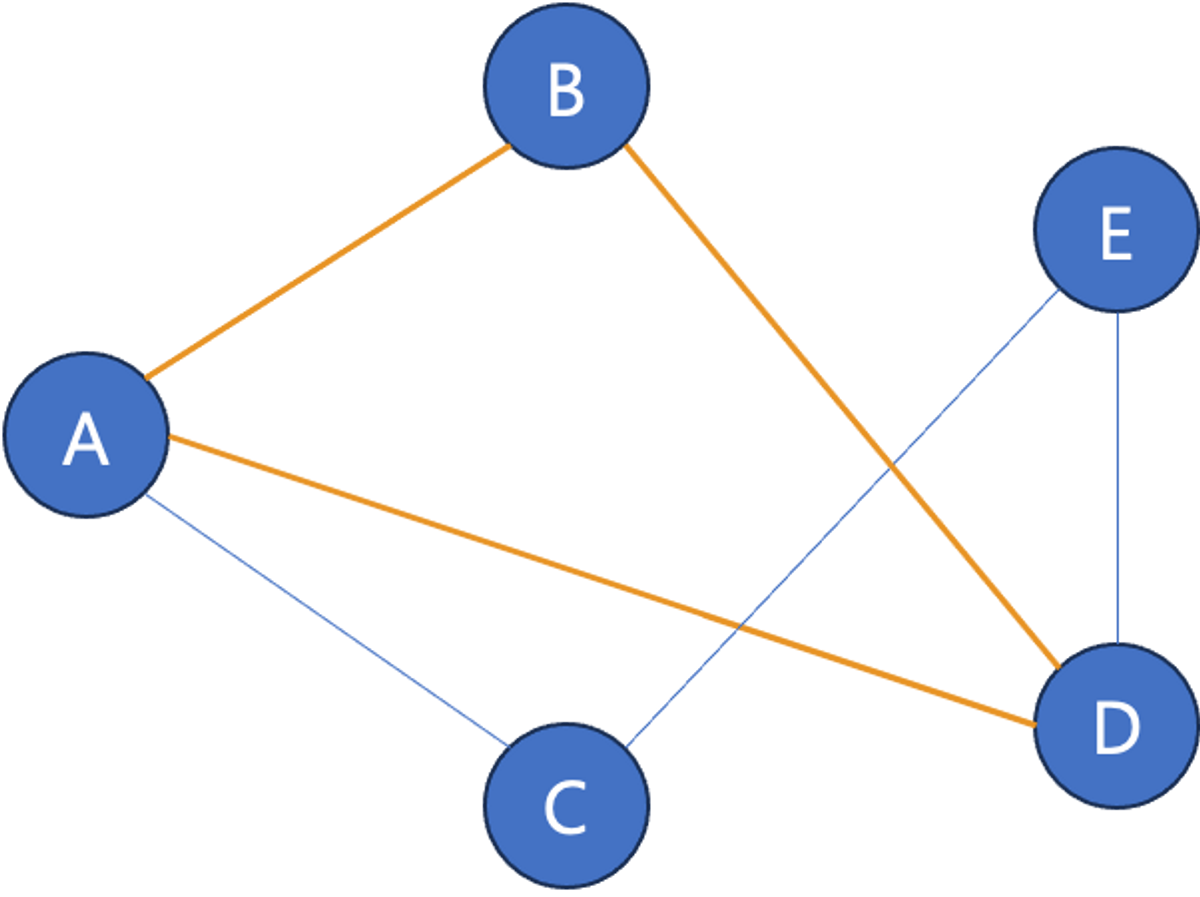
시작한 정점에서 끝나는 경로를 사이클(순환)이라고 합니다. 이러한 순환 구조를 가진 그래프를 순환 그래프라고 합니다.
경로 중 시작 정점과 끝 정점이 같은 경우를 순환 그래프라고 한다. 위의 그림은 경로가 A,D,B,A처럼 될 경우 순환 그래프라고 할 수 있다.
- 완전 그래프
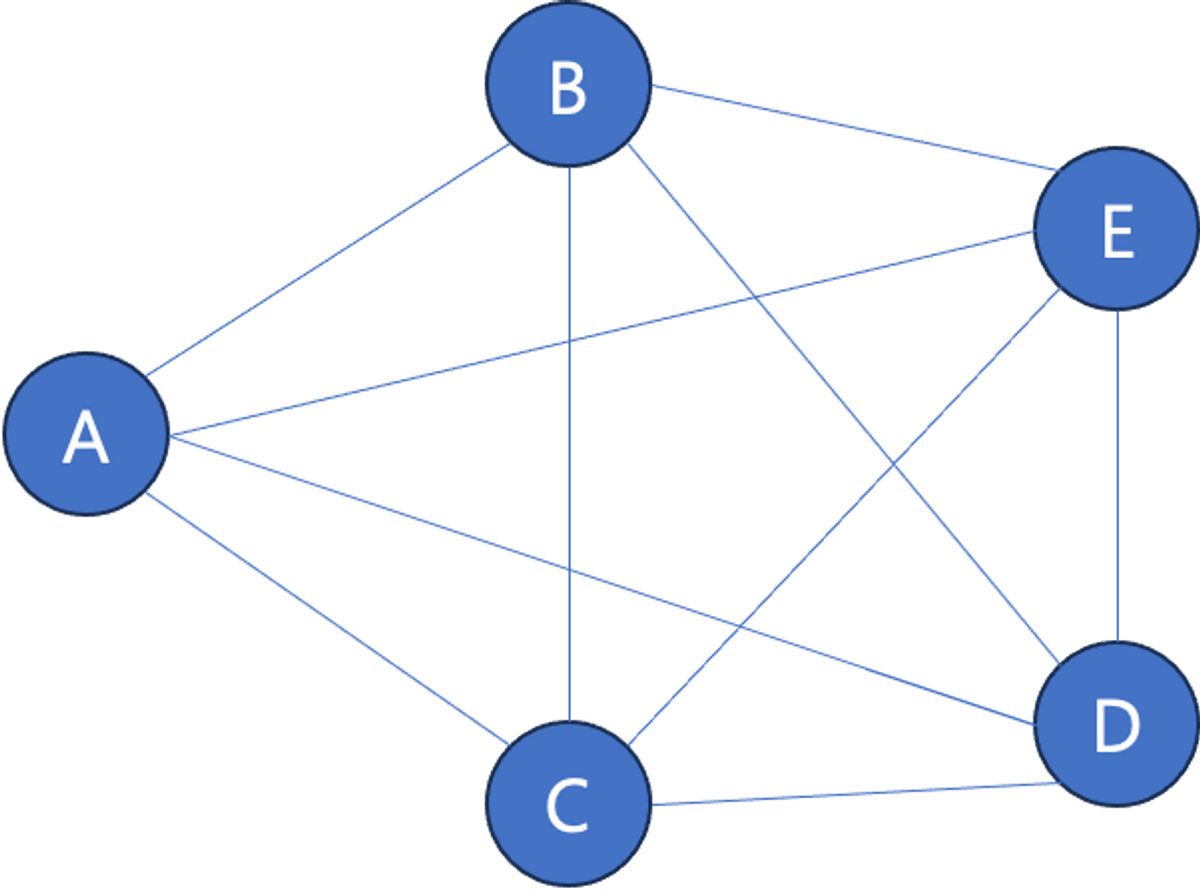
정점들에 대해 가능한 모든 간선을 가진 그래프입니다.
완전 그래프는 간선의 수가 최대이며, 정점의 수가 n개이면 Kn으로 표현한다.
위의 그림은 정점의 수가 5개이며, 이 경우 $K_5$으로 표현한다.
정점의 수 : V
간선의 수 : V*(V-1)/2
✅ 그래프의 표현
- 인접 행렬

정점의 갯수를 V라고 할 떄, V*V 크기의 2차원 배열을 이용해서 간선 정보를 저장.
인접 행렬에서 행과 열은 번호를 의미하며, 각 원소들은 정점 간 간선을 표현한다.
- 그래프가 가중치가 없다면 boolean (0, 1) 으로 연결 정보를 표현
- 가중치가 있다면 각 간선의 가중치를 배열로 저장한다.
장점
연결 확인 : 노드 간의 연결 여부를 $O(1)$ 시간에 확인 가능
정보 확인: 간선의 가중치나 부가 정보를 배열 요소로 표현하여 $O(1)$ 시간에 확인 가능
간선 추가/제거: 간선의 추가/제거가 용이
단점
공간 복잡도: 노드의 개수가 많거나 간선의 수가 많은 경우 공간 복잡도가 $O(N^2)$ 될 수 있음
노드 추가 / 제거의 비효율성 : 노드가 추가 또는 삭제될 때마다 배열의 크기를 변경해야 함
인접행렬실습
package graph;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class AdjacentMatrix {
public void solution() throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
// StringTokenizer: 입력받은 문자열을 ' ' (또는 지정된 delimiter) 를 기준으로 나누어서
// 한 단어씩 반환해주는 도구
StringTokenizer graphTokenizer // 8 10
= new StringTokenizer(reader.readLine());
// StringTokenizer.nextToken(): 다음 단어를 가져오기
int maxNodes = Integer.parseInt(graphTokenizer.nextToken()); // 8
int edges = Integer.parseInt(graphTokenizer.nextToken()); // 10
// 인접 행렬: 2차원 배열
// 만약 노드가 1부터 N + 1 까지라면
// 계산할때 매번 -1을 해주거나
// 인접 행렬을 한칸 더 늘리거나
int[][] adjMatrix = new int[maxNodes][maxNodes]; // 0 ~ 7 까지 표현 가능한 인접 행렬
// 간선의 갯수만큼 반복해서 입력을 받는다.
for (int i = 0; i < edges; i++) {
// 다음줄을 단어 단위로 나눠주는 Tokenizer
StringTokenizer edgeTokenizer
= new StringTokenizer(reader.readLine());
// 입력 줄의 첫 숫자
int startNode = Integer.parseInt(edgeTokenizer.nextToken());
// 입력 줄의 두번째 숫자
int endNode = Integer.parseInt(edgeTokenizer.nextToken());
// 유향 그래프의 경우 아래줄 만
adjMatrix[startNode][endNode] = 1;
// 무향 그래프의 경우 아래줄도 함께
adjMatrix[endNode][startNode] = 1;
}
for (int[] row: adjMatrix) {
System.out.println(Arrays.toString(row));
}
}
public static void main(String[] args) throws IOException {
new AdjacentMatrix().solution();
}
}
// 입력
8 10
0 1
0 2
0 3
1 3
1 4
2 5
3 4
4 7
5 6
6 7
// 출력
[0, 1, 1, 1, 0, 0, 0, 0]
[1, 0, 0, 1, 1, 0, 0, 0]
[1, 0, 0, 0, 0, 1, 0, 0]
[1, 1, 0, 0, 1, 0, 0, 0]
[0, 1, 0, 1, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1, 0, 1]
[0, 0, 0, 0, 1, 0, 1, 0]
인접 리스트
'Algorithm' 카테고리의 다른 글
| 백준 10818 최소, 최대 (0) | 2023.07.09 |
|---|---|
| 백준 10828 스택 (0) | 2023.07.09 |
| 브루트 포스 Brute Force 알고리즘 (0) | 2023.07.09 |
| 버블정렬, 선택정렬, 계수정렬 알고리즘 (0) | 2023.07.09 |
| 이진트리탐색 (Binary Search Tree) 알고리즘 (0) | 2023.06.22 |
